锦标赛排序

2021-02-28

锦标赛排序和树形选择排序

锦标赛排序也叫树形选择排序，是一种按照锦标赛的思想进行选择的排序方法，该方法是在简单选择排序方法上的改进。简单选择排序，花费的时间大部分都浪费在值的比较上面，而锦标赛排序刚好用树保存了前面比较的结果，下一次比较时直接利用前面比较的结果，这样就大大减少比较的时间，从而降低了时间复杂度，由$O(n^2)$降到$O(nlogn)$，但是浪费了比较多的空间，“最大的值”也比较了多次。

大概过程如下：

首先对n个记录进行两两比较，然后优胜者之间再进行两两比较，如此重复，直至选出最小关键字的记录为止。

类似甲乙丙三队比赛，前提是有这样一种传递关系：若乙胜丙，甲胜乙，则认为甲必能胜丙。

锦标赛排序图解如下

初始序列，这么多队伍参加比赛

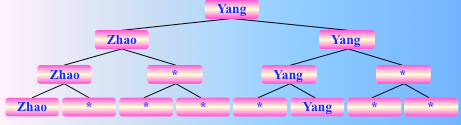
两两比较之，用一个完全二叉树表示，反复直到一趟比较后，选出冠军

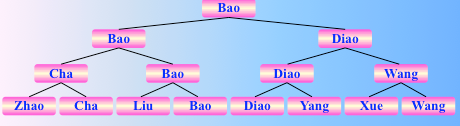
找到了 bao，是冠军，选出冠军的比较次数为 $ 2^2+2^1+2^0 = 2^3 -1 = n-1$，然后继续比较，把原始序列的 bao去掉

选了 cha，选出亚军的比较次数为 $3$，即 $log2 n$ 次。同理，把 cha去掉，继续两两比较

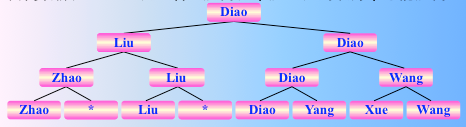
找到了 diao，其后的 $n-2$ 个人的名次均如此产生

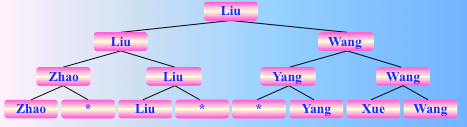
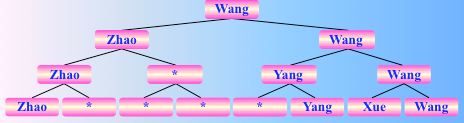
所以对于$n$ 个参赛选手来说，即对 $n$ 个记录进行锦标赛排序，总的关键字比较次数至多为 $(n-1)log2 n + n -1$，故时间复杂度为：$ O(nlogn)$。

此法除排序结果所需的 $n$ 个单元外，尚需 $n-1 $个辅助单元。

这个过程可用一棵有$n$个叶子结点的完全二叉树表示，根节点中的关键字即为叶子结点中的最小关键字。在输出最小关键字之后，根据关系的可传递性，欲选出次小关键字，仅需将叶子结点中的最小关键字改为“最大值”，如$∞$，然后从该叶子结点开始，和其左（右）兄弟的关键字进行比较，修改从叶子结点到根的路径上各结点的关键字，则根结点的关键字即为次小关键字。也就是所谓的树形选择排序，这种算法的缺点在于：辅助存储空间较多、最大值进行多余的比较。


/** 
     * --------------------------------------- 
     * 树形选择排序 ：
     * 对于简单排序来说，主要是进行n-1趟元素的比较，每趟比较n-2次，
     * 每趟比较取出一个最小值(也可以是最大值)，逐步使列表有序。
     * 但是第一趟的比较是可以为后续的比较提供信息的，使后续的比较次数大大减少，
     * 而后续的比较又可以为更后续的比较提供信息，这样就减少了比较的次数，减少了
     * 时间复杂度。
     * 
     * 实现原理：
     * 第一步，首先对n个记录进行两两比较，得到较小的n/2个数再依次比较，依次类推
     * 直到得到一个最小值,这是一个构造完全二叉树的过程，根节点即为最小元素，叶子节点为列表元素。
     * 构造的此树的存储结构可以用数组表示方法，数组长度为2n-1。填充此树，比如
     * 列表元素为：49    38     65    97   76    13    27   49
     * 构造的树为：                     13
     *                     38               13
     *                38       65       13       27
     *              19  38   65  97   76  13   27  49
     * 13为根结点位最小值，列表元素为叶子节点
     * 
     * 第二步，移走最小元素，此时可重新为数组a的第一个位置赋值为此最小值，
     * 之后如果找出次小值则可以为第二个位置赋值，......
     * 
     * 第三步，找出次小值，找出最小值在叶子节点的位置，从该节点开始，和其兄弟节点
     * 进行比较，修改从叶子节点到根节点的元素值，比较完毕后，根节点为次小值。
     * 第三步比较是利用了第一次比较提供的信息，因为第一步已经得到了两两比较的
     * 较小值，只要拿第一次与最小值比较的元素(即最小值的兄弟节点)与它们比较即可得最小值。
     * 即拿上述例子的76与27比较，然后27与38比较得到次小值27。
     * 重复第二和第三步，排序完成。
     * 
     * PS:这里把移出去的叶子节点都要重设为最大值，可对此方法进行稍微改动
     * 可传一个最大值进来，这里是整型所以用了Integer.MAX_VALUE
     */  
public class TreeSort {

    public static void treeSelectSort(Object[] a) {
        int len = a.length;
        int treeSize = 2 * len - 1;  //完全二叉树的节点数
        int low = 0;
        Object[] tree = new Object[treeSize];   //临时的树存储空间
        //由后向前填充此树，索引从0开始
        for (int i = len - 1, j = 0; i >= 0; --i, j++) {   //填充叶子节点
            tree[treeSize - 1 - j] = a[i];
        }
        // 两两比较，结果到上一层节点
        for (int i = treeSize - 1; i > 0; i -= 2) {  //填充非终端节点
            tree[(i - 1) / 2] = ((Comparable) tree[i - 1]).compareTo(tree[i]) < 0 ? tree[i - 1] : tree[i];
        }

        //不断移走最小节点
        int minIndex;
        while (low < len) {
            Object min = tree[0];  //最小值
            a[low++] = min;
            minIndex = treeSize - 1;
            //找到最小值的索引
            while (((Comparable) tree[minIndex]).compareTo(min) != 0) {
                minIndex--;
            }
            tree[minIndex] = Integer.MAX_VALUE;  //设置一个最大值标志
            //找到其兄弟节点
            while (minIndex > 0) {  //如果其还有父节点
                if (minIndex % 2 == 0) {  //如果是右节点
                    tree[(minIndex - 1) / 2] = ((Comparable) tree[minIndex - 1]).compareTo(tree[minIndex])
                            < 0 ? tree[minIndex - 1] : tree[minIndex];
                    minIndex = (minIndex - 1) / 2;
                } else {  //如果是左节点
                    tree[minIndex / 2] = ((Comparable) tree[minIndex]).compareTo(tree[minIndex + 1])
                            < 0 ? tree[minIndex] : tree[minIndex + 1];
                    minIndex = minIndex / 2;
                }
            }

        }
    }
}